Game Component: Spaceship editor, part 3 #
I've been trying out a few ideas with quick & dirty demos to see if they're at all promising as part of a game. Two posts ago I talked about a spaceship editor, where you could place the thrusters, and the “AI” would learn how to pick thrusters that most closely matched your desired motion. In the last post I spent some time describing how I spent some time trying to figure out the characteristics of the ship, how I learned more about the problem I needed to solve, and some of the things I tried to find a “nice” solution to the math. I was really happy with the things I had worked on. However…
The real questions I wanted to answer were:
- Is it actually fun to fly a ship with this physics model?
- Is it actually fun to design a ship? In other words, are there interesting designs and tradeoffs?
Somewhere during the process I realized that getting the “nice” solution wasn't that important, and I had probably spent too much time on it. (Reading this article reminds me that I get distracted too easily on fun problems and I have trouble completing things.) I wasn't getting closer to answering the important questions. Instead, I was having fun learning some math that I had forgotten 15 years ago. Having fun learning math isn't bad; it's just not the main goal.

To answer the first question, I spent some time in various ships just flying around. My conclusion was yes, it's fun to fly around in a world by itself, but no, it doesn't seem like it'd be fun in an actual game, where there are other things to do. And that's when it hit me: all that time I spent thinking about the math might have been a waste of time (except that it was a lot of fun to learn some math); I should first make sure I can make the ships fun to fly.
I flew around a lot and thought about what bugged me. The main problem was that inertia was fun at first but it seemed to get annoying after a little while. For example, if I'm moving forwards with W, and then I rotate left with A, I'm still moving, but my jets are pointed at an angle. To stop moving you need to use a combination of S and Q. Even worse, since it's a keyboard instead of an analog controller, you can't hit the right mix of the two to make yourself stop.
In addition, it wasn't clear to me whether the controls should set acceleration, velocity, or target position. Acceleration was the most natural thing, and that's what I started with. But that means when you hit any key, you start out slow, then go faster and faster, until it's out of control. That might be realistic but it's not much fun. I switched it to setting velocity. But what velocity should I target? I arbitrarily chose some multiple K of the acceleration, so that after K time you'd reach that velocity.
I also needed to do more tuning. The mass, moment of inertia, friction, and rotation/translation tradeoffs are set arbitrarily. I had tried adjusting this but none of the parameters were quite right, and every time I changed the physics it got worse, and I had to tune to make it better again.
I tried to answer the second question (whether there are interesting ship tradeoffs) by creating several ships. Based on that experience, my answer is maybe. The ships I made are noticeably different but I have a clear favorite. If there's only one best ship then the ship editor's not going to be interesting. The problem is that the answer to the second question depends on what I do with the physics.
So I decided to work on the physics first.
I tried tackling inertia directly, with some ideas from a friend:
Inertia in World Coordinates gives me realistic physics for flying ships. This is what I had started with, and this is what I was unhappy with. When you're going north, and turn left, you keep flying north. The inertia keeps moving you north, even if you face west.
Inertia in Ship Coordinates gives me something that behaves more like a vehicle on wheels. When you're going north, and turn left, you start going west. The inertia keeps moving you forwards, whatever direction that may be.
No Inertia would mean that you only move when thrusters are fired. This is the most extreme change but if inertia is really a problem then it's worth a try.
I also tried treating rotation differently from x and y, because rotation seems to lead to some of the situations that make the ship less fun to control.

It was only after playing with the various options that I learned that I do really want inertia in world coordinates. Sometimes I just have to try something to help me learn something (also see this blog post). Having no inertia, or inertia in ship coordinates, just didn't feel fun to fly at all, and that's not what I would've predicted. I had the right form of inertia; something else was wrong.
After all the testing, I realized I wanted inertia but not the full effect. At low speeds, inertia is great, but at high speeds, inertia is less fun. With inertia alone it takes as long to speed up as it does to slow down again. It's okay if it takes a second or two to reach a high speed. But when I let go of the keys I want the ship to come to a stop pretty quickly. I added a force to slow the ship down. I tried three approaches:
Constant force decreases velocity V by up to K. This can be interpreted as surface friction.
Linear force decreases velocity V by K*V. I don't know what this might correspond to in physics, but in the calculations it corresponds to “reducing” inertia.
Quadratic force decreases velocity V by K*V*V. This can be interpreted as air resistance.
All three of them helped. After trying and tuning the three I decided that the linear force reduction was the most pleasant, but still not ideal. With quadratic, the problem I ran into (which I might have predicted if I were smarter) was that you can't increase your maximum velocity much if you add thrusters. Instead, it was largely determined by the air resistance. That would be fine if I were creating just one ship, but for the ship editor to be interesting, I need the number and power of the thrusters to actually matter! Constant friction left too much of your motion determined by inertia at higher speeds. The linear slowdown felt the best. I can't justify it if I were going for realism, but I'm going for fun, not realism.
I think flying the ship can be made fun. The next question to tackle is whether there are interesting tradeoffs in ship design.
Game Component: Spaceship editor, part 2 #
In the last post, I described a fun problem I wanted to play with, and my initial attempt to solve it. I made several ships, figured out how their thrusters worked, and built a simple system for flying. The keys were W for forwards, S for backwards, Q for slide left, E for slide right, A for rotate left, and D for rotate right. Once I flew them around and saw that it was fun, and ship design might be interesting for the player, I wanted to understand better the characteristics of the ships. So I did something that often helps me: visualize the data.
In this diagram you can see the black dots are the possible outputs for the first test ship, viewed from three different perspectives. You can see that it's not completely random. There's a definite shape there. The variety of shapes is what makes this problem interesting. I plotted these for all of my test ships, and learned a lot. For example, look at the lower left plot (with the A–D + W–S axes). From it we can learn that the ship flies forwards quickly (W) but backwards slowly (S). It can rotate left (A) and right (D) slowly. Going forwards makes it easier to rotate quickly; going backwards makes it harder.

While flying the ship I noticed however that there was a second problem I hadn't appreciated at first. When choosing outputs that are “close” to the desired output, a difference of +3 to +4 is nowhere near as significant as a difference of 0 to +0.1. When the player wants zero movement, it's very important to keep it zero. If one key is pressed down, then there should be one non-zero in the output; if two keys are pressed then there should be two non-zeros. The most common case for the random input/output pairs is to have no zeros, but the most common case for the player is to be pressing just one key, and thus needing two zeros!

Because my random input/output approach was fun but didn't handle the one and two-keystroke cases well, I also looked a few different analytical approaches to compute the reverse mapping directly. I looked at the pseudo-inverse operation, which is like matrix inverse but works with non-square matrices. However, it didn't look like it would help me. I also looked at it as a linear programming optimization problem. That approach looked promising but the Simplex algorithm was more than I wanted to implement.
None of the mathematical approaches I saw directly matched the problem I was trying to solve. It's easy to add the constraint about zeros to a linear programming problem but not to the matrix pseudo-inverse. It might be made to work with the random input/output pairs, by adding some weights to the output components, but the outputs generated from random inputs almost never contained zeros, so I'm never going to get exactly what I want.
One of my habits that seems to work well for me is to alternate between working things out on paper and writing code. The ship thruster physics, the input/output pairs, and the matrix math I first worked on paper, then implemented it. So I went back to paper and pen for this problem. Can I increase the number of outputs that contain some zeros?
First I tried changing the way I picked random inputs, and favored 0 and 1 instead of evenly uniformly choosing any number between 0 and 1. That didn't help much (but I later had an insight related to this change, so maybe it was useful after all). I decided I needed to attack the problem directly. The idea of interpolating between output points was still in my head, and I used that here. If I picked two points on opposite sides of a zero plane, I could find some interpolation that was on the plane. I took pairs of the random input/output pairs and solved for any zeros on the line between them. This worked well! I now had a new set of points that had one zero in the output. By applying the algorithm again, I could find a set of outputs that had two zeros.
In this diagram you can see the black dots are the random outputs projected down to the three planes, and also the white dots, which are formed from finding the point in between two black dots that intersects the plane. The space covered by white dots is more limited than that for black dots. That's because there are some wild movements that can't be controlled if you try to restrict one of the outputs to zero.
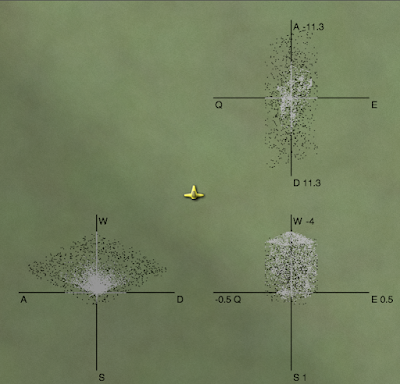
I had up to 1000 random input/output pairs. Solving the equations for every zero plane and every pair that was on opposite sides of the plane meant I needed to solve a matrix equation around 750,000 times. It took a while but it was reasonable. Applying this again to get the outputs with two zeros would've been too slow. And I wanted this to be fast enough so that you could see the flight characteristics as you were editing the spaceship.
Have you ever noticed that you often find something or think of something only after you stop looking for it? I've noticed that this happens for me when solving problems. I had gotten stuck with the brute force technique and I needed something smarter, but I was getting nowhere. So I stopped working on the problem. A few days later, while playing a game, I had an insight that should have been obvious from the start.
All the random inputs are thruster settings from 0.0 to 1.0. We're taking matrix M and multiplying it by a vector T, which must be in a fairly small space. If there are N dimensions, T is an N-dimensional vector, and all its components are between 0.0 and 1.0. That means … the space of all valid thruster configurations is a unit N-dimensional hypercube.
A wise man once told me that it's sometimes easier to solve the general case than the specific case. I had been trying to solve the specific case, of a single input mapped to a single output. And then I'm using computational power to handle lots of them. The general case is to take the entire hypercube and transform it to the output, and see what comes out.
What comes out is a polyhedron in 3 dimensions.
This insight seemed like it came out of nowhere, while I was playing a game, killing orcs. But when I thought about it more, I think it wasn't out of nowhere. If I were smarter I would've figured it out from the very beginning, but some things I had thought touched on the hypercube approach. One clue was that when I picked random numbers for inputs, I found that it useful to bias towards 0.0 and 1.0. My experiments were guiding me towards choosing the vertices of the hypercube. Another clue was that in linear programming, you can think of the valid space as a convex polyhedron in some higher dimensional space. I had spent some time thinking about what the polyhedron represented in my problem but I wasn't able to make the connection. A third clue was that plotting the black and white dots made it look like there were simple polygons involved.
For N thrusters the hypercube has 2N vertices. In this diagram you can see the hypercube vertices, multiplied by the matrix, do cover the space that the random points covered. As before, the black dots are the random sample. The colored dots are the vertices of the hypercube.

Instead of picking lots of random points, I should pick these points. And then I can take every pair of these and find the interpolation that has a zero output. And then I can take every pair of those and find the outputs with two zeros.

I worked this out on paper. Page after page of solving equations for test ship 1, following by plotting things out on graph paper, convinced me that this was quite promising.
I was really happy with myself. I had figured out a much more elegant
solution that didn't involve random numbers.
I took the equations I solved on paper and wrote some code to solve them. I tried it out on several different ships. And then I ran into a problem. For one of my ships, with 8 thrusters, the algorithm still ran rather slowly. Why? Well, 28 is 256. Finding the one-zero outputs involved examining 215 pairs in 3 dimensions, or around 100,000 systems of equations to solve. It took a few seconds, but I hadn't gotten to the one-zero case yet, which is the really expensive one. For this ship I was almost as slow as the random point approach. The random points were slow but equally slow for all ships, whereas the hypercube vertices got worse every thruster you added. Ick. While starting a cube lamp on my desk, I realized that all the useful zeros should occur along edges, not as interpolations between two arbitrary points. I could reduce 28 pairs X 27 pairs to just 28 pairs X 8. Much faster! However, that was only the one-zero outputs. I still had to run the interpolations again, to find the two-zero outputs. And even with the optimization that was around 1,000,000 systems of equations. I was sure there was another optimization involving surfaces instead of edges but I just couldn't figure out what it was.
So I took another break. I spent some time plotting what I had, to see if there were insights I could draw from the visualization. I plotted sets of points and found that many of them just aren't relevant because they're in the “interior” of the areas. All I care about is the perimeter. To compute the perimeter in two dimensions is a well-known problem: convex hull.
I thought about how to compute a convex hull, and it seemed rather simple. I wrote down my notes, then proceeded to see what the standard algorithms were. None of them seemed as simple as my algorithm, which meant my algorithm probably has a bug. But I couldn't see what it was, so I decided to let it wait a bit. A few days later, still unable to think of a flaw, I sketched out the math on paper, then implemented it. Although I had a few bugs in the code, the algorithm itself worked.
Once I had the convex hull algorithm available, my next step was to use it to simplify the one-zero outputs into a convex hull before finding the two-zero points.
In this diagram you can see the points that make up the convex hull. As before, the white dots are the interpolations between random points, to find positions on the zero plane. The colored points with black borders around them are the interpolations between hypercube vertices, fed into the convex hull algorithm. You can see that all the points I computed from the random set lie within the convex hull computed from the hypercube vertices.

In fact the two-zero points always occur between adjacent points in the convex hull, so I had gotten yet another optimization out of this change. However, I discovered that my convex hull algorithm does have a flaw. When there are collinear points it doesn't always remove all of them. The flaw remains in my code; it doesn't seem to be a big deal in practice, because my code is now “fast enough”. For each of the five test ships, generating the flight parameters takes less than a second.
Another thing that wasn't clear to me when I started was that when you press both W and Q, you want to go both left and forwards, but there's not a fixed ratio between the two. Sometimes you can get both and sometimes you have to make a tradeoff, and none of the techniques worked out of the box for that. I think this might be something to leave to the ship designer, once the flight characteristics are known. For example, in the above diagrams you could have a way to mark what you want a combination of keys to do.
It's been a fun journey. I've taken off some rust from my skills. And I learned a bit more about linear programming, the simplex algorithm, physics, and convex hulls.
However, I haven't yet written an editor. But I now have the physics and math worked out, so once I have an editor, you'll be able to see the flight characteristics of the ship you're editing. I'll post the demo and source here. It will be nice if there are interesting tradeoffs for the player. For example, if you put jets on the wingtips, you can rotate very quickly, but perhaps it adds a lot of mass to make the wings sturdy enough to take jets, and that extra mass slows you down in terms of forward acceleration. Once I have the editor I'll get a better feel for whether there are interesting tradeoffs to be made, and whether this would be useful to have in a game.
Game Component: Spaceship editor, part 1 #
I've been playing Spore recently. It's an interesting game. One of the criticisms is that the physical characteristics of the things you do in the editor don't make a difference to gameplay. For example, having wide legs or narrow legs or four legs or six legs doesn't affect your speed. Only the +Speed items affect speed. Only in the Cell stage does placement matter. I read some of their reasoning behind this design and I agree with it. In a game where creativity is more important than realism, simplifying that aspect of the game will encourage people to be more creative in their designs. I know that if the number of legs actually mattered for gameplay, I wouldn't have made my creature hop around on one leg.
Although I think they made the right decision for Spore, I was inspired to explore the alternative: something where the way you design your creature matters a great deal. To fit in with the 2d top-down theme I've been using (see the space station miniproject), I'm using spaceships instead of creatures.
The main idea for this miniproject is that you'd design the ship, and then the “AI” would learn how to fly the ship you designed. For example, let's consider the following ship with four thrusters:
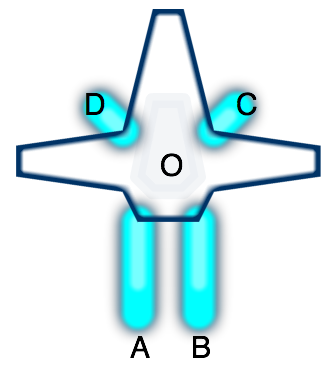
If you fire either thruster A or B, you'd end up rotating. But if you
fire both at once, you would go forwards. Given a set of thrusters
(location on the ship, direction they fire, and their maximum power),
I can calculate the effect on the ship (acceleration and rotational
acceleration). Initially I was calculating the force to be only what
was transmitted along the A→O vector, but later I realized that
because the ship is rigid, the entire force gets transmitted to the
entire ship, and is independent of the location of the thruster.
Since thruster A fires in direction (0, +2), the force on the ship is
(0, -2). Rotation is slightly trickier, as we need to calculate
torque, and take into account the rotational moment of inertia. For
now I'm assuming the mass and moment of inertia are constants, but
later I'll compute these based on the characteristics of the ship. The
torque does take into account the position of the thruster, and we
have to compute the cross product of the A→O vector (-2, 4) and the
force vector (0, -2).
The forward mapping from thrusters to forces turns out to be a matrix multiplication. Each thruster is a column and each effect on the ship is a row. Doing this for each of the thrusters, we get the thruster matrix M mapping thrusters to force and torque:
| M: | A | B | C | D |
|---|---|---|---|---|
| Fx | 0 | 0 | -0.5 | 0.5 |
| Fy | -2 | -2 | 0.5 | 0.5 |
| Tq | 10 | -10 | 1.25 | -1.25 |
Given a thruster configuration vector T, M∙T gives us the forces acting on the ship.
The real problem though is reversing that mapping. The player presses a key to move forwards, and I need to figure out which combination of thrusters best accelerates the ship forwards. What value of T leads to M*T being close to [ 0 1 0 ]?
The simplest approach is brute force. So I started with that first. I generated lots of random inputs and calculated their outputs. Then when I needed some particular output, I scanned them all and picked the input that most closely generated that output. Over multiple simulation cycles, any errors would be corrected by picking different input/output pairs. I could make this even more stable by iterating within a single simulation cycle, and interpolating among the results.
This approach worked reasonably well!
The ship behavior was interesting. My first test ship (the one I'm using for these examples) moved reasonably well forwards and backwards, and could rotate well, but it couldn't slide left and right quickly.
My second ship is a variant of the first. When moving forwards it can rotate well, but if you're stationary or going backwards the rotation is limited. When you fly it you'll see that if you want to rotate, you need to move forwards at the same time. Here's what it looks like:

My third ship had reasonable movement, and rather asymmetric: it could rotate and slide left at the same time, or rotate and slide right at the same time, but it was much slower if you rotated left while sliding right or vice versa. It looks a little different from the first two, but right now that makes no difference in the physics:

My fourth ship is a damaged version of the third ship, to see if having inoperable thrusters would make for interesting gameplay. Going forwards would also make you spin around in circles. It was fun to play with in the prototype but I'm not convinced it'd be fun in a game. You can see why it's unstable:

My fifth test ship could rotate very quickly but couldn't go backwards at all (at least until I fixed a bug in the physics calculations), so you'd turn around and go forwards in order to stop moving. This might be a ship you can't build until later stages of the game, when you've gained building points or parts or money. Just look at how much power it has:

At this point the prototype made me think there was something potentially fun for a game. You could design your own ship and make tradeoffs. The game “AI” would learn how to map your keys to thruster movements, and the player would then have to learn best to use the controls for navigation and combat. For example, having to turn a ship around to stop is unusual but you might design a ship that way if you could get lightning-quick rotation in return. You might design different ships for different levels. Or you might learn how to play a ship so well that you don't want to switch to something else with different characteristics.
I knew the ships were all different in their behaviors but I didn't understand what their limits were. So my next step was to try to understand the flight characteristics of the ships. That's for the next post.