Game Component: Spaceship editor, part 2

From Red Blob Games's Blog

In the last post, I described a fun problem I wanted to play with, and my initial attempt to solve it. I made several ships, figured out how their thrusters worked, and built a simple system for flying. The keys were W for forwards, S for backwards, Q for slide left, E for slide right, A for rotate left, and D for rotate right. Once I flew them around and saw that it was fun, and ship design might be interesting for the player, I wanted to understand better the characteristics of the ships. So I did something that often helps me: visualize the data.

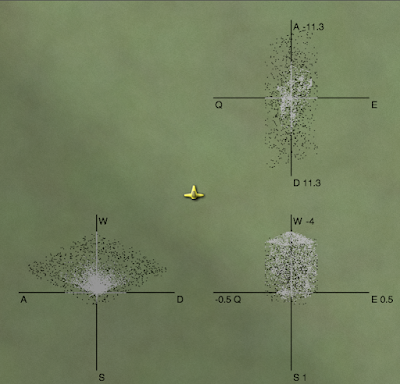
In this diagram you can see the black dots are the possible outputs for the first test ship, viewed from three different perspectives. You can see that it's not completely random. There's a definite shape there. The variety of shapes is what makes this problem interesting. I plotted these for all of my test ships, and learned a lot. For example, look at the lower left plot (with the A–D + W–S axes). From it we can learn that the ship flies forwards quickly (W) but backwards slowly (S). It can rotate left (A) and right (D) slowly. Going forwards makes it easier to rotate quickly; going backwards makes it harder.

While flying the ship I noticed however that there was a second problem I hadn't appreciated at first. When choosing outputs that are “close” to the desired output, a difference of +3 to +4 is nowhere near as significant as a difference of 0 to +0.1. When the player wants zero movement, it's very important to keep it zero. If one key is pressed down, then there should be one non-zero in the output; if two keys are pressed then there should be two non-zeros. The most common case for the random input/output pairs is to have no zeros, but the most common case for the player is to be pressing just one key, and thus needing two zeros!

Because my random input/output approach was fun but didn't handle the one and two-keystroke cases well, I also looked a few different analytical approaches to compute the reverse mapping directly. I looked at the pseudo-inverse operation, which is like matrix inverse but works with non-square matrices. However, it didn't look like it would help me. I also looked at it as a linear programming optimization problem. That approach looked promising but the Simplex algorithm was more than I wanted to implement.

None of the mathematical approaches I saw directly matched the problem I was trying to solve. It's easy to add the constraint about zeros to a linear programming problem but not to the matrix pseudo-inverse. It might be made to work with the random input/output pairs, by adding some weights to the output components, but the outputs generated from random inputs almost never contained zeros, so I'm never going to get exactly what I want.

One of my habits that seems to work well for me is to alternate between working things out on paper and writing code. The ship thruster physics, the input/output pairs, and the matrix math I first worked on paper, then implemented it. So I went back to paper and pen for this problem. Can I increase the number of outputs that contain some zeros?

First I tried changing the way I picked random inputs, and favored 0 and 1 instead of evenly uniformly choosing any number between 0 and 1. That didn't help much (but I later had an insight related to this change, so maybe it was useful after all). I decided I needed to attack the problem directly. The idea of interpolating between output points was still in my head, and I used that here. If I picked two points on opposite sides of a zero plane, I could find some interpolation that was on the plane. I took pairs of the random input/output pairs and solved for any zeros on the line between them. This worked well! I now had a new set of points that had one zero in the output. By applying the algorithm again, I could find a set of outputs that had two zeros.

In this diagram you can see the black dots are the random outputs projected down to the three planes, and also the white dots, which are formed from finding the point in between two black dots that intersects the plane. The space covered by white dots is more limited than that for black dots. That's because there are some wild movements that can't be controlled if you try to restrict one of the outputs to zero.

I had up to 1000 random input/output pairs. Solving the equations for every zero plane and every pair that was on opposite sides of the plane meant I needed to solve a matrix equation around 750,000 times. It took a while but it was reasonable. Applying this again to get the outputs with two zeros would've been too slow. And I wanted this to be fast enough so that you could see the flight characteristics as you were editing the spaceship.

Have you ever noticed that you often find something or think of something only after you stop looking for it? I've noticed that this happens for me when solving problems. I had gotten stuck with the brute force technique and I needed something smarter, but I was getting nowhere. So I stopped working on the problem. A few days later, while playing a game, I had an insight that should have been obvious from the start.

All the random inputs are thruster settings from 0.0 to 1.0. We're taking matrix M and multiplying it by a vector T, which must be in a fairly small space. If there are N dimensions, T is an N-dimensional vector, and all its components are between 0.0 and 1.0. That means … the space of all valid thruster configurations is a unit N-dimensional hypercube.

A wise man once told me that it's sometimes easier to solve the general case than the specific case. I had been trying to solve the specific case, of a single input mapped to a single output. And then I'm using computational power to handle lots of them. The general case is to take the entire hypercube and transform it to the output, and see what comes out.

What comes out is a polyhedron in 3 dimensions.

This insight seemed like it came out of nowhere, while I was playing a game, killing orcs. But when I thought about it more, I think it wasn't out of nowhere. If I were smarter I would've figured it out from the very beginning, but some things I had thought touched on the hypercube approach. One clue was that when I picked random numbers for inputs, I found that it useful to bias towards 0.0 and 1.0. My experiments were guiding me towards choosing the vertices of the hypercube. Another clue was that in linear programming, you can think of the valid space as a convex polyhedron in some higher dimensional space. I had spent some time thinking about what the polyhedron represented in my problem but I wasn't able to make the connection. A third clue was that plotting the black and white dots made it look like there were simple polygons involved.

For N thrusters the hypercube has 2^N vertices. In this diagram you can see the hypercube vertices, multiplied by the matrix, do cover the space that the random points covered. As before, the black dots are the random sample. The colored dots are the vertices of the hypercube.

Instead of picking lots of random points, I should pick these points. And then I can take every pair of these and find the interpolation that has a zero output. And then I can take every pair of those and find the outputs with two zeros.

I worked this out on paper. Page after page of solving equations for test ship 1, following by plotting things out on graph paper, convinced me that this was quite promising.

I was really happy with myself. I had figured out a much more elegant solution that didn't involve random numbers.

I took the equations I solved on paper and wrote some code to solve them. I tried it out on several different ships. And then I ran into a problem. For one of my ships, with 8 thrusters, the algorithm still ran rather slowly. Why? Well, 2⁸ is 256. Finding the one-zero outputs involved examining 2¹⁵ pairs in 3 dimensions, or around 100,000 systems of equations to solve. It took a few seconds, but I hadn't gotten to the one-zero case yet, which is the really expensive one. For this ship I was almost as slow as the random point approach. The random points were slow but equally slow for all ships, whereas the hypercube vertices got worse every thruster you added. Ick. While starting a cube lamp on my desk, I realized that all the useful zeros should occur along edges, not as interpolations between two arbitrary points. I could reduce 2⁸ pairs X 2⁷ pairs to just 2⁸ pairs X 8. Much faster! However, that was only the one-zero outputs. I still had to run the interpolations again, to find the two-zero outputs. And even with the optimization that was around 1,000,000 systems of equations. I was sure there was another optimization involving surfaces instead of edges but I just couldn't figure out what it was.

So I took another break. I spent some time plotting what I had, to see if there were insights I could draw from the visualization. I plotted sets of points and found that many of them just aren't relevant because they're in the “interior” of the areas. All I care about is the perimeter. To compute the perimeter in two dimensions is a well-known problem: convex hull.

I thought about how to compute a convex hull, and it seemed rather simple. I wrote down my notes, then proceeded to see what the standard algorithms were. None of them seemed as simple as my algorithm, which meant my algorithm probably has a bug. But I couldn't see what it was, so I decided to let it wait a bit. A few days later, still unable to think of a flaw, I sketched out the math on paper, then implemented it. Although I had a few bugs in the code, the algorithm itself worked.

Once I had the convex hull algorithm available, my next step was to use it to simplify the one-zero outputs into a convex hull before finding the two-zero points.

In this diagram you can see the points that make up the convex hull. As before, the white dots are the interpolations between random points, to find positions on the zero plane. The colored points with black borders around them are the interpolations between hypercube vertices, fed into the convex hull algorithm. You can see that all the points I computed from the random set lie within the convex hull computed from the hypercube vertices.

In fact the two-zero points always occur between adjacent points in the convex hull, so I had gotten yet another optimization out of this change. However, I discovered that my convex hull algorithm does have a flaw. When there are collinear points it doesn't always remove all of them. The flaw remains in my code; it doesn't seem to be a big deal in practice, because my code is now “fast enough”. For each of the five test ships, generating the flight parameters takes less than a second.

Another thing that wasn't clear to me when I started was that when you press both W and Q, you want to go both left and forwards, but there's not a fixed ratio between the two. Sometimes you can get both and sometimes you have to make a tradeoff, and none of the techniques worked out of the box for that. I think this might be something to leave to the ship designer, once the flight characteristics are known. For example, in the above diagrams you could have a way to mark what you want a combination of keys to do.

It's been a fun journey. I've taken off some rust from my skills. And I learned a bit more about linear programming, the simplex algorithm, physics, and convex hulls.

However, I haven't yet written an editor. But I now have the physics and math worked out, so once I have an editor, you'll be able to see the flight characteristics of the ship you're editing. I'll post the demo and source here. It will be nice if there are interesting tradeoffs for the player. For example, if you put jets on the wingtips, you can rotate very quickly, but perhaps it adds a lot of mass to make the wings sturdy enough to take jets, and that extra mass slows you down in terms of forward acceleration. Once I have the editor I'll get a better feel for whether there are interesting tradeoffs to be made, and whether this would be useful to have in a game.

Labels: flash , ideas , project