Brainstorming with factoring #
In the last post I described how I sometimes describe a problem with a matrix, and then look at the matrix transpose to see if it gives me new ideas. Another technique I use is to look for a factoring.
In algebra, factoring transforms a polynomial like 5x² + 8x - 21 into (x + 3)·(5x - 7). To solve 5x² + 8x - 21 = 0, we can first factor into (x + 3)·(5x - 7) = 0. Then we say that x + 3 = 0 or 5x - 7 = 0. Factoring turns a problem into several easier problems.
| x | 3 | |
|---|---|---|
| 5x | 5x² | 15x |
| -7 | -7x | -21 |
Let's look at an example: I have six classes, File, EncryptedFile, GzipFile, EncryptedGzipFile, BzipFile, EncryptedBzipFile. I can factor these into a matrix:
Brainstorming with transpose #
Sometimes I get stuck and look for a way to think about a problem a different way. There are some problems that you can view in the form of a matrix/table. The structure looks like this:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | A1 | B1 | C1 | D1 | E1 |
| 2 | A2 | B2 | C2 | D2 | E2 |
| 3 | A3 | B3 | C3 | D3 | E3 |
| 4 | A4 | B4 | C4 | D4 | E4 |
| 5 | A5 | B5 | C5 | D5 | E5 |
There are rows and columns, and I'm trying to work on the cells. Let's try an example from a simple game:
| Attack | Defend | Special | |
|---|---|---|---|
| Fighter | sword | armor | slam |
| Mage | fireball | reflect | freeze |
| Thief | dagger | dodge | disarm |
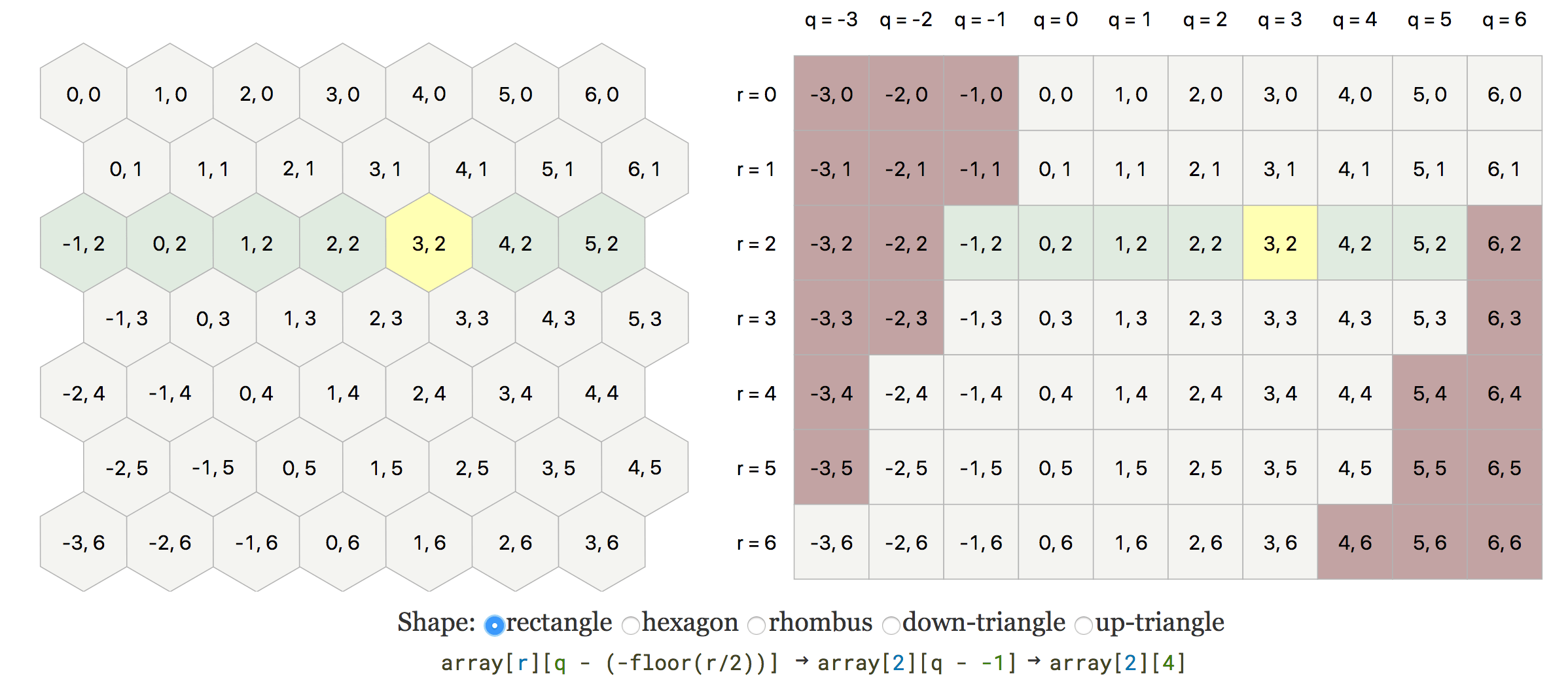
Improving hexagon map storage diagram #
Last week, I decided to improve the map storage section of the hexagon guide. This section had a diagram that suggested the use of a 2D array, but then it presented formulas that didn't look like what was shown. Reader feedback made me realize this section was confusing. I was mixing two separate steps here.
- Store the map in a 2D array.
- Slide the rows to the left to save space.
Labels: hexagons
Improving island shaping for map generation #
One of my goals for 2019 is to improve my existing pages. This week I improved the island map section of my noise-based map generation page.

Labels: maps