On my hexagon grid guide I have a function to convert pixel (cartesian) coordinates to hexagon "cube" coordinates. I reuse a hex_round() function that I needed for line drawing. However, there are many other algorithms out there that work differently. I had made a list on a separate page. But I hadn't actually implemented them … until now.
I decided to implement five of the algorithms, and ended up implementing ten of them (but publishing only nine, because I couldn't get one of them to work). Several of them didn't quite match up with my original algorithm but I didn't understand why. My first thought was to have an interactive diagram where you can point at any pixel and get back the hex coordinates. I thought it might help me understand what's going on. But the ladder of abstraction page reminds me that sometimes I can display all the values instead of one at a time. So I made a static diagram using this coloring:

This worked pretty well. I could immediately see various errors:
- white hexagon not in the center → I have the translation wrong
- hexagons are the wrong size → I have the scale wrong
- hexagons are stretched or squashed → I have the x/y scale wrong
- hexagon coloring wrong → coordinate system didn't match mine
- pattern not even hexagons → something went horribly wrong!
It worked much better than interactively testing one pixel at a time.
I added interactivity as well, as it was simple to add. The interactivity helped me realize that my visual test was passing even though the coordinates were wrong. Oops! It turns out that some of my outputs were flipped left/right or top/bottom and I didn't realize it with a symmetrical test pattern. So I changed the color on two hexagons so that I could more easily spot problems like this (see the red in the lower left and pink in the lower right):

With that I was able to spot and fix the remaining errors.
Or did I?
I did not.
Visual tests are nice for trying to figure out what's going on, but it's easy to miss small differences. Ideally, I'd test every pixel with every algorithm against the "correct" answer. But I don't actually know which algorithm is most correct. There are boundary cases where it's ambiguous. So the next step was to mark the pixels where any algorithm disagreed:
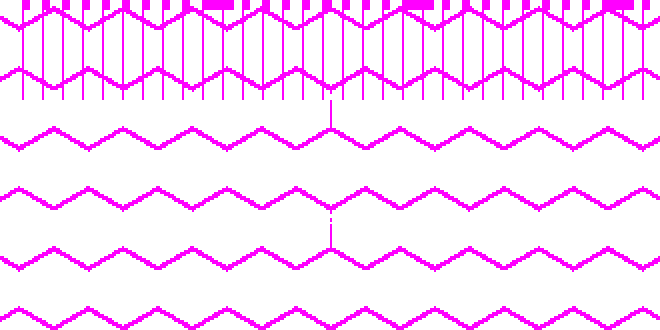
Wow, this was quite a surprise. There are several patterns here that warrant further investigation. The rectangles at the top are a mystery. The vertical lines at the top suggest that there may be something working differently with negative Y coordinates. The horizontal squiggles suggest there's an inconsistent Y offset in one of the algorithms. But which algorithms are producing these differences?
I investigated and found that I had introduced a bug in one of the algorithms. I also seemed to have a bug in my test code. After fixing those, the remaining differences were either at corners, or along edges in the hex_round() algorithm. I'm pretty happy with that test. I also printed out the number of pixels where the output differs so that I could know if there was even 1 pixel off.
I'm glad I finally implemented these algorithms. I've found some on the web and some are sent in by readers. Justin Pombrio's page and James McNeill's page were especially nice. There are still plenty more algorithms that I could implement, but after implementing ten of them I'm ready to do something else for a while.
Take a look at the implementation page to see the algorithms and the code.
Labels: hexagons
Post a Comment