In the previous two posts I described how I sometimes approach a problem by trying to arrange it into a matrix. Sometimes that doesn't work and I instead try to look at the problem backwards. As an example, consider procedural map generation. I often start with a noise function, adding octaves, adjusting parameters, and adding layers. I'm doing this because I'm looking for maps with certain properties.
It's fine to start by playing with parameters, but the parameter space is rather large, and it's unclear whether I'll actually find the parameters that best match what I want. Instead, after playing around a bit, I stop and think in the opposite order: if I can describe what I want, it might help be find the parameters.
This is actually the motivation I was taught for algebra. Given an equation like 5x² + 8x - 21 = 0, what is x? When I didn't know algebra, I would've solved this by trying a bunch of values for x, jumping randomly at first, then adjusting it once I felt I was getting close. Algebra gives us the tool to go in the other direction. Instead of guessing at answers, it gives me tools (factoring, or the quadratic equations, or Newton's iterative root finding) that I can use to more intelligently find the values of x (-3 or 7/5).
I feel like I often am in that same situation with programming. For procedural map generation, after tweaking parameters for a while, I stopped to list some things I wanted for the game worlds in one project:
- Players should start far apart on the beach.
- Players should move uphill as they level up.
- Players shouldn't reach the edge of the map.
- Players should join into groups as they increase in level.
- Beaches should have easy monsters without much variation.
- Midlands should have a wide variety of monsters of medium difficulty.
- Highlands should have hard "boss" monsters.
- There should be some landmark to help players stay at the same difficulty level, and another landmark to help players go up or down in difficulty level.
That list led to some constraints:
- The game worlds should be islands with a lot of coastline and a small peak in the center.
- Elevation should match monster difficulty.
- Low and high elevation should have less biome variation than middle elevations.
- Roads should stay at a fixed difficulty level.
- Rivers should flow from high to low elevation, and give players a way to navigate up/down.
The constraints then led me to design the map generator. This led to a much better set of maps than the ones I got by tweaking parameters like I usually do. And the resulting article has gotten lots of people interested in Voronoi-based maps.
Another example is unit tests. I'm supposed to come up with a list of examples to test. For example, for hexagonal grids I might think of testing that add(Hex(1, 2), Hex(3, 4)) == Hex(4, 6) . Then I might remember to test zeros: add(Hex(0, 1), Hex(7, 9)) == Hex(7, 10). Then I might remember to test negative numbers too: add(Hex(-3, 4) + Hex(7, -8)) == Hex(4, -4). Ok, great, I have a few unit tests.
If I think more about this, what I really am testing is add(Hex(A, B), Hex(C, D)) == Hex(A+C, B+D). I came up with the three examples based on this general rule. I'm working backwards from this rule to come up with the unit tests. If I can directly encode this rule into the test system, I can have the system itself work backwards to come with the instances to test. This is called “property based testing”. (Also see: metamorphic testing)
Another example is constraint solvers. In these systems you describe what you want in the output, and the system comes up with a way to satisfy the constraints. From the Procedural Content Generation Book, chapter 8:
In the constructive methods of Chapter 3 and the fractal and noise methods of Chapter 4, we can produce different kinds of output by tweaking the algorithms until we’re satisfied with their output. But if we know what properties we’d like generated content to have, it can be more convenient to directly specify what we want, and then have a general algorithm find content meeting our criteria.
In Answer Set Programming, explored in that book, you describe the structure of what you're working with (tiles are floors or walls, and the tiles are adjacent to each other), the structure of solutions you're looking for (a dungeon is a bunch of connected tiles with a start and an end), and the properties of the solutions (side passages should be at most 5 rooms, there are 1 or 2 loops, there are three henchmen to defeat before you reach the boss). The system then comes up with possible solutions and lets you decide what to do with them.
A recent constraint solver got a lot of attention because of its cool name and demos: Wave Function Collapse. You give it example images to tell it what the constraints on adjacent tiles are, and then it comes up with more examples that match your given patterns. There's a paper, WaveFunctionCollapse is Constraint Solving in the Wild, that describes how it works:
Operationally, WFC implements a non-backtracking, greedy search method. This paper examines WFC as an instance of constraint solving methods.
I done much with constraint solvers yet. As with Algebra, there's a lot for me to learn before I can them effectively.
Another example is when I made a spaceship where you could drag the thrusters to wherever you wanted, and the system would figure out which thrusters to fire when you pressed W, A, S, D, Q, E. For example, in this spaceship:

If you want to go forwards, you'd fire the two rear thrusters. If you want to rotate left, you'd fire the rear right thruster and the front left thruster. I tried to solve this by having the system try lots of parameters:
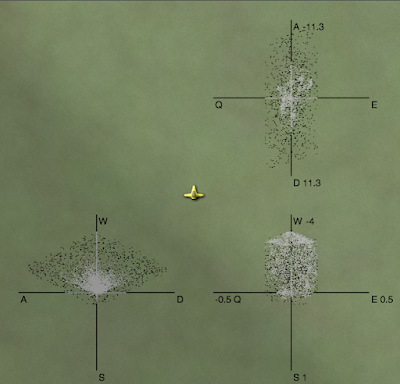
It worked, but it wasn't great. I realized later that this too is another instance of where working backwards would have helped. It turns out the movement of the spaceships could be described by a linear constraint system. Had I realized it, I could've used an existing library that solves the constraints exactly, instead of my trial-and-error approach coming up with an approximation.
Yet another example is the G9.js project, which lets you drag the outputs of some function around on the screen, and it will figure out how to change the inputs to match your desired output. The demos of G9.js are great! Be sure to uncomment the "uncomment the following line" on the Rings demo.
Sometimes it's useful to think about a problem in reverse. I often find that it gives me better solutions than if I only consider the forward direction.
Post a Comment