Hex grids: code generator #
In the last post I described how I had expected to generate lots of algorithm variants, but ended up discovering a better approach. The new system is different from the system I used when I wrote the hex grid guide. It's simpler and more modular, and I have ideas for making it even simpler. If I am able to simplify enough, I may not need to generate algorithms dynamically. In any case, the final step is to convert the algorithms in abstract format into a specific programming language.
Transforming the algorithms into code was easier than figuring out how to structure the algorithms, but it was also more tedious. For expressions, it's pretty straightforward. A syntax tree like Add(Name("x"), Int(3)) turns into x+3 in Python/C/Java/JS or (+ x 3) in Racket/Scheme/Lisp/Clojure. For statements, it's pretty straightforward too, but there are a few more differences between languages, including indentation and placement of braces. For declarations, languages start differing more, with functions, structs, classes, methods, modules, namespaces, etc. I wanted to generate code that uses each language's canonical style, including naming conventions and comments. I'll show some examples, using the distance function:
Function("cube_distance", Int, [Param("a", Cube), Param("b", Cube)], Return( Int( Divide( Add( Add(Call("abs", Subtract(Field("a", "x"), Field("b", "x"))), Call("abs", Subtract(Field("a", "y"), Field("b", "y")))), Call("abs", Subtract(Field("a", "z"), Field("b", "z"))) ), Int(2) ) ) ) )
- Python
- Python uses
/for float division and//for integer division. My syntax tree does not. Instead, when I see a patternCall(Int, Divide(a, b))I want to outputa//binstead ofint(a/b). This shows up in the distance function:def cube_distance(a, b): return (abs(a.x - b.x) + abs(a.y - b.y) + abs(a.z - b.z)) // 2
Python doesn't need a separate class to hold int and float coordinates, so
FractionalCubeshould be merged intoCube.
- C++
- C++ uses
/for float division and/for integer division, but it depends on the types of the operands. My syntax tree doesn't track the types of the subexpressions, so I don't know which I'll get. As a result, I end up with an unneccessaryint()in the distance function:int cube_distance(Cube a, Cube b) { return int((abs(a.x - b.x) + abs(a.y - b.y) + abs(a.z - b.z)) / 2); }
- Racket
- Division is tricky here too. Racket uses
quotientinstead of/when the result is going to be an integer. Like Python's output, I can look forCall(Int, Divide(a, b))and output(quotient a b)instead of(truncate (/ a b)). Racket also supports multi-argument addition, so I could convert(+ (+ a b) c)into(+ a b c). Here's the distance function in Racket:(define (cube-distance a b) (quotient (+ (abs (- (cube-x a) (cube-x b))) (abs (- (cube-y a) (cube-y b))) (abs (- (cube-z a) (cube-z b)))) 2))
The naming convention is
cube-distanceinstead ofcube_distance.
- C#, Java
- Declarations are different here. Instead of top-level functions, I need to make everything into a method. For now, I'm using static methods, but it might make sense to use instance methods for some of the algorithms. Here's what distance looks like in C#:
public class Cube { ... static public int Distance(Cube a, Cube b) { return (int)((Math.Abs(a.x - b.x) + Math.Abs(a.y - b.y) + Math.Abs(a.z - b.z)) / 2); } }
Instead of
cube_distance, I should useCube.Distancein C# andCube.distancein Java.
The differences between languages got larger as I moved to bigger functions. The sequence and record data types translate easily: C++ arrays/structs, Python lists/records, C# arrays/classes, Racket vectors/structs. But some algorithms use sets and maps, and it's less clear what types to use there. For Racket and Haskell, I want to use a more functional style, but for C++ and Python, I use an imperative style. In the end:
- I didn't implement the more complex algorithms. They're harder, and I decided I should prioritize getting the simple ones working across many languages and many grid types. If I had known this from the beginning, I would've used a simpler proto-algorithm approach.
- I didn't implement the more complex approach of adapting code for each grid type. Instead, I used the simpler approach of having each grid type convert to Cube coordinates, and then use the cube algorithms. If I had known this from the beginning, I would've written the algorithms by hand instead of writing a proto-algorithm to algorithm conversion step.
- I didn't implement all the grid types. Instead of all the variants of Cube, Axial, and Offset, I only implemented one Cube variant, one Axial variant, and two Offset variants. If I had known this from the beginning, I would've written a simpler system.
- The code for Axial coordinates is mostly different from the code for Offset coordinates. I was expecting more code to be shared. This made think that I probably shouldn't treat these two the same.
- I now realize that my choice of Cube/Axial isn't great. Instead of q=x, r=z I should have picked q=x, r=y! I could have switched the y and z axes on the cube diagram. If I merge Cube and Axial I'll make this change then.
- I wrote the proto-algorithms expecting that I'd output functional style (Racket, Haskell), object-oriented style (C#, Java, Haxe), and module style (C++, Python, Javascript). Looking back, I probably should have used object-oriented style everywhere. The style differences somewhat complicated things.
- I also wrote the proto-algorithms expecting that I'd use them on the page itself, and also convert them to code for a downloadable library. That complicated things. I should have focused on downloadable libraries.
- The code generator for Racket mostly works but it wasn't a purely functional style (because my "proto-algorithms" are imperative). I had planned to make the standard algorithms work in a purely functional style but some of the more complex algorithms will probably be too much work to justify a separate version. Looking back, I shouldn't have spent time trying to figure out a functional style for Racket; it wasn't worth spending time on a different style for just one language.
- I didn't implement variants in code style, such as indentation and brace placement. When I started the project it seemed like it would be cool, but it just doesn't seem important anymore.
- I didn't implement a "pro" version of the code that would use small arrays with 2 or 3 elements instead of named fields. Thinking of them as arrays or matrices would also potentially allow SIMD or GPU instructions. Pointy vs flat variants become an index swizzle. Converting hex to pixel and pixel to hex become matrix multiplies.
It's been a fun project, and as usual there are so many more things I want to do with this, but there are so many other things I want to do too, so I want to wrap this up.
- Should I switch to the simpler system that merges Axial and Cube together? This will require a major update to the hex grid guide. It would make my advice much simpler. Instead of "use Cube for calculations and Axial for storage" I could say "use Axial everywhere". However, I'm worried that it will annoy anyone who's using the current hex grid page, because the new system will be incompatible.
- Should I treat pointy vs flat as an x/y switch or as a 90° rotation? I am leaning towards x/y switch. I will also have to switch q/r to keep q being "columns" and r being "rows".
What's my next step? Testing. I have unit tests for the generated code, and they all pass, but I want to test the code in a real project. What real project do I have? The hex grid page itself. I'm going to replace the hand-written hex grid code for the page with the generated code. This will give me confidence that I have the right design and set of algorithms.
What are other things I need to do before I publish? Add comments to the generated code, implement more outputs (Javascript, Typescript, Java, Objective C, Racket), add an option for overloaded operators (+ and ==) in languages where that's standard style, and figure out instance vs class methods.
That's it for now. My blog posts aren't polished but I hope they give you a "behind the scenes" view of the stuff that goes through my head and the things I try while working on these projects. I also find that trying to write down what I'm doing helps me work out the design and details, and this series of posts was no exception. By "thinking out loud" I've been able to resolve some of the issues I had been trying to figure out. I hope to have the rest of the code generator finished in a few weeks.
Hex grids: choosing data structures and generating algorithms #
In the last blog post I described the project I've been working on: generating hex grid code libraries, for lots of different types of hex grids. I wanted to transform "proto-algorithms" into algorithms for a specific type of hex grid, and then convert the algorithm into code.. That was the pattern I initially expected to follow, so I'd end up with maybe 50 algorithms multiplied by 70 grid types multiplied by 20 languages, or a total of 70,000 code snippets.
I tried experimenting with other hex grid algorithms to see how they might transform depending on geometry, and realized that most of them don't work like the hex distance example in the previous blog post. I spent some time looking at all the algorithms to determine:
- Do I want to transform the code handling cube coordinates into code handling each other coordinate system? Code to code transforms are hard.
- Do I want to transform the data for other coordinate systems into data for cube coordinates, then run an algorithm for cube coordinates? Data to data transforms are easy.
- Does it even make sense to run the algorithm in a non-canonical coordinate system? Many of the algorithms are best with with cube coordinates.
- Does the algorithm work purely on the grid system, or does it also involve how the hex is drawn on the screen? Most of the algorithms do not involve the screen layout.
I concluded that I had vastly overestimated the number of different algorithms that need to be generated. Many of the variants end up being exactly the same code. For example, I wanted to generate variants for people who have a y-axis pointing up vs down, but only two of the algorithms have to change; all the others can stay the same. Also, it is a lot of work for me to transform the code handling cube coordinates into code handling other systems, but a compiler's optimizer can do all that work for me for free if I use data-to-data transforms. I shouldn't bother writing code-to-code transforms.
While trying to figure out the best way to write the variants, I ended up with this structure:
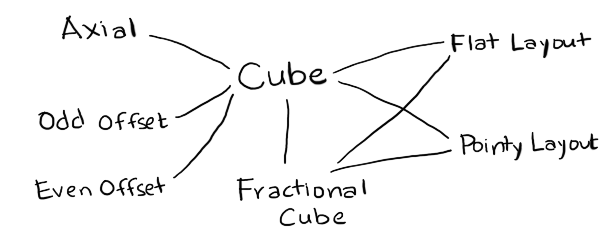
- Cube
- is the canonical coordinate system used for algorithms. I've implemented only one of many variants.
- FractionalCube
- is used to represent non-grid locations. I needed this for line drawing and for pixel to hex conversion.
- Hex
- is the coordinate system used for storage. I've implemented Axial (only one variant) and Offset (even and odd parity).
- Layout
- is used to convert from hexes to screen coordinates for drawing and from screen coordinates to hexes for mouse clicks. I've implemented Pointy and Flat topped hex layouts.
- Point
- is the coordinate system for screen coordinates. This will typically come from your graphics library, but for the generated code I've included a placeholder data structure.
To implement these, I wanted a language that lets me work easily with abstract syntax trees. My usual choices are PLT Scheme (Racket) or ML (OCaml). Scheme is a little nicer for this because it gives me an easy way to define the proto-algorithms using macros so that I don't have to write my own parser. For this particular project though I wanted to run the code generator on the server (to generate all variants and run unit tests on the generated code) and in the browser (to generate custom code based on your preferences). I chose Haxe, an ML-influenced language with the programming features I wanted (tagged unions and pattern matching and macros) and also the platform features I wanted (can run on the server but can also generate Javascript to run in the browser). Also, my hex grid code is already written in Haxe, so I was hoping to be able to reuse it for the proto-algorithms.
I wrote code that reads function definitions and outputs code to generate the syntax trees for those definitions. For example, if I write x+3, Haxe will give me something like EBinOp(OpAdd, CIdent("x"), CInt(3)). I want to produce something like Add(Name("x"), Int(3)), so I need the macro to return something like ECall(CIdent("Add"), [ECall(CIdent("Name"), [CString("x")]), ECall(CIdent("Int"), [CInt(3)])]). I have code that reads code and generates code that generates code. Scheme/Racket is an ideal language for that kind of thing.
In the process of implementing the proto-algorithm to algorithm compiler, I made some discoveries and realizations:
- My diagrams are written in Javascript, which doesn't have a separate int and float type, but in many languages I need to distinguish these. As a result, I created a type
FractionalCubewith floats that's separate fromCubewith ints.FractionalCubeis used for two main algorithms, pixel to hex and line drawing, and both of those need a helper routine, hex rounding. - I realized that my explanation for pointy vs flat top hexagons is inconsistent. In one section, I claim it's a rotation of 30°. In other sections, I claim the algorithms are simply different. In my underlying code, I often swap x and y. The code is simplest if swapping x and y, or rotating 90°, but the names of axes stay most consistent (q for columns, r for rows) if I rotate by 30°. I don't know which I should use.
- It's also possible to generalize even further, and rotate by any angle. This is less "simple" because it means I need to insert an additional rotation step in a few places, but it's more general. I'm not yet ready to switch to this.
- In the offset grid section, I claim that there are four types, odd-r, even-r, odd-q, and even-q. However, if pointy vs flat is a swapping of x and y (instead of a rotation by 30°), then odd-r and odd-q are related by swapping both x/y and q/r. Much simpler! This means there are really only two offset types, odd-parity and even-parity.
- It's also possible to generalize even further, and say that the offset can be by any odd number. The odd-parity (odd-r and odd-q) variants become an offset by -1 and the even-parity (even-r and even-q) variants become an offset by +1. This simplifies even more. I'm not yet ready to switch to this.
- The remaining grid variants involve renaming the axes and changing their signs. I'd like to implement this at some point, but I don't know if it's really worth it.
- Cube and Axial coordinate systems are pretty much the same, except Cube explicitly stores the third coordinate, and Axial calculates it when needed. It might make sense to merge the two, and call the axes q, r, s. I need to think about this more.
- Offset and Axial share much less code than I had expected. One of the algorithms (
hex_direction) doesn't work with offset grids, and two of the algorithms (hex_neighborandhex_add) have different implementations for offset and axial. If I merge Cube and Axial, then Offset would be its own thing. I need to think about this more. - It's pretty clean to separate out anything involving the screen from everything else, which only involves the grid. This means variants like the y-axis pointing up or down go away, except for a small part of the code. Screen transformations include translations (centering hex 0,0 at x,y other than 0,0), scaling (setting the size of the hex, including hexes that are taller or shorter than usual), rotations (primarily 90° but any angle is possible), and transformations for isometric views.
I started this project thinking I would need to generate lots of algorithms. I thought the algorithm generation step would take the most work, and the code generation step would be relatively easy. I ended up spending a lot more time thinking about how to represent the modules. I don't actually need to generate lots of algorithms. Instead, I am considering changing the page to use a simpler approach:
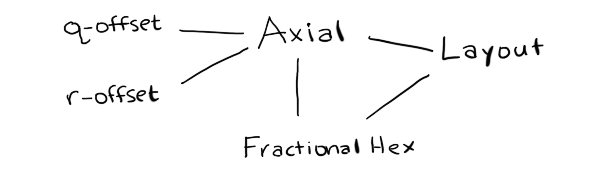
If I do that, it will be a major change to the hex grid guide.
In the next post I'll talk about the code generation.
Hex grids: procedurally generating code #
I've been questioning some of my approach to writing tutorials. Most of the time I provide algorithms, math, and pseudocode but not runnable code. Part of the reason is that I've been on so many platforms and languages in the past, and I don't want to spend time on things that are useful today but not five years from now. Part of the reason is that I learn better by studying pseudocode and producing runnable code. And part of the reason is that many of the topics I cover (pathfinding, simulation, AI) aren't really about code, but about techniques that are useful when writing code. Most of it has to be adapted for each game.
Hex grids are different though. There's not as much to be learned by studying the code; I think most of it is learned through the diagrams and explanations. Adaptation is sometimes tricky, and I don't want you spending your time on trivial bugs like missing a negative sign. So I decided to try, for this one page, providing some useful code.
Which language? Which platform? Which of the 70+ grid types? How many combinations of these can I practically provide code for?
Well, of course, the solution is procedural generation, right? Right??
I attempted to procedurally generate downloadable libraries to handle hex grids.
The plan was:
- Write some "proto-algorithms" that could work with any geometry.
- Ask the reader about the geometry of hex grids being used.
- Mix the "proto-algorithm" with a description of the geometry, generating algorithms in some abstract format.
- Ask the reader about the programming language and style.
- Turn the generated algorithms into downloadable code.
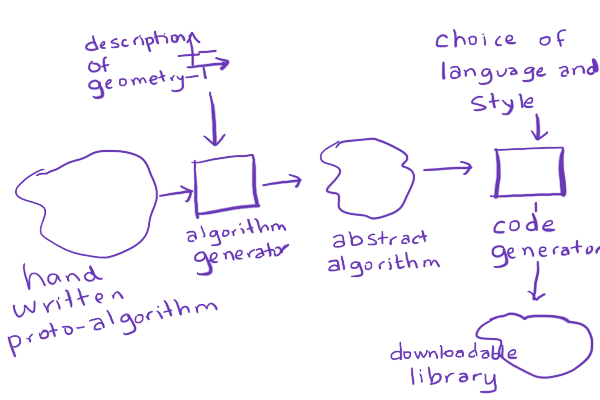
For example, I would write a "proto-algorithm" by hand for hex distances:
/* Distance between two hexes */ function hex_distance(a, b) { var ac = cube(a); var bc = cube(b); var dx = ac.x - bc.x; var dy = ac.y - bc.y; var dz = ac.z - bc.z; return abs(dx) + abs(dy) + abs(dz); }
Let's say that the reader uses an axial coordinate system where x=q, y=-r, z=r-q. This is different from the one I use in my hex grid guide. So if you wanted to take the hex distance algorithm from my page and adapt it for this coordinate system, it'd be a little tricky, with some renaming and sign flipping. I should be able to generate it instead, by inlining the cube conversion:
function hex_distance(a, b) { var ax = a.q; var ay = -a.r; var az = a.r - a.q; var bx = b.q; var by = -b.r; var bz = b.r - b.q; var dx = ax - bx; var dy = ay - by; var dz = az - bz; return abs(dx) + abs(dy) + abs(dz); }
and then simplifying that code:
function hex_distance(a, b) { var dx = a.q - b.q; var dy = -a.r + b.r; var dz = a.r - a.q - b.r + b.q; return abs(dx) + abs(dy) + abs(dz); }
and simplifying more:
function hex_distance(a, b) { return abs(a.q - b.q) + abs(b.r - a.r) + abs(a.r - a.q - b.r + b.q); }
Then if the reader says, I want Java code for this, with three space indentation, I could convert this abstract format into Java code:
public abstract class AbstractSpringBeanFactoryProxy { ... }
No, no, not like that! Sorry. ;-) How about this:
public class Hex { public int q, r; ... /** * Distance between two hexes */ public static distance(Hex a, Hex b) { return Math.abs(a.q - b.q) + Math.abs(b.r - a.r) + Math.abs(a.r - a.q - b.r + b.q); } ... }
Wouldn't that be cool? Custom-built algorithms for your choice of hex grid, in your choice of language, in your preferred programming style? With comments? And if I'm generating code that could be error-prone, I should have unit tests too, right? And of course I should procedurally generate the unit tests. And if I'm generating unit tests, I should generate all possible grid variants and all possible languages on the server, and compile and run the unit tests, so that I make sure that whichever choices the reader makes, the code will be correct.
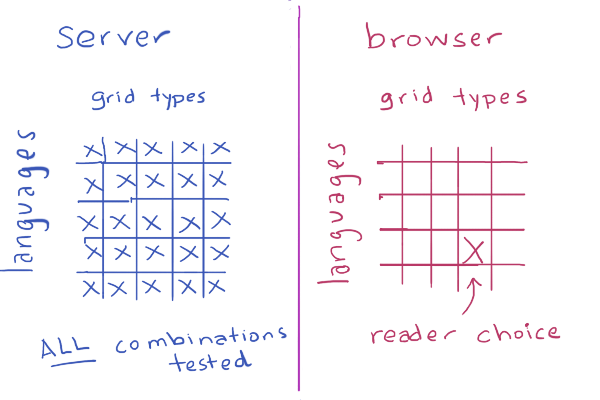
I knew it was a little ambitious, and probably way overkill, but I decided to try anyway.
Well, as expected, I didn't succeed. In the next blog post, I'll describe what happened.
Hex grids: simplifying the variants #
On the original hex grid guide I had claimed there were over 70 variants of hex grids. Most of these turn out to be merely a different choice of axes, either by renaming them or by negating the sign. Here are some variants of offset coordinates:
And here are some variants of axial coordinates:
Axial and Cube are really the same, except Cubes explicitly store the third coordinate and in Axial we calculate it in the accessor, when needed.
Why would you want some of the other labelings? If I use an alternate labeling of offset coordinates, I can rotate the entire grid from pointy top to flat top and back:
This simplifies the math. It means I no longer need to treat pointy and flat top hexes separately, but instead I can focus on just a few basic grid types (cube, axial, even offset, odd offset) and then produce the pointy and flat top from those. I can further simplify by merging axial and cube together. I don't yet know if I want to do that. Can I merge even and odd offset? Yes, probably, but I think I won't right now.
Pointy top vs Flat top is a rotation. I had originally claimed it was a rotation of 30° but it is simpler to think of it as a rotation of 90°. It's even simpler to think of it as a permutation of x,y into y,x (renaming axes). There are also several coordinate systems that I don't cover on the page, and don't plan to anytime soon. However I might add a supplemental page that describes them.
I believe the new descriptions of coordinate systems will be simpler than the previous ones. However, they're also different, and I worry about changing the system that I've described in some incompatible way.
- Should I unify Axial and Cube?
- Even if I don't, should I rename Cube's coordinates from x,y,z to q,r,s? That way they match up more closely, and Cube is no longer confused with cartesian coordinates.
- Should I unify even Offset (even-q, even-r) and odd Offset (odd-q, odd-r)? I think the math is slightly uglier but it'd work just fine.
- Should I try to support all possible axis assignments, or just some "canonical" ones like I do now?
- Should I try to preserve the specific choices of axes on the current page, or choose the ones that make things simpler?
Update: [2015-03-28] I'm no longer convinced that swapping x,y is the easiest way to deal with pointy vs flat top. It's the simplest implementation, but it causes "q" and "r" to no longer correspond to "column" and "row", and I think it might be worth preserving that mnemonic. A 90° rotation is nice to implement too but I think the 30° rotation best preserves q/r.