Around a month ago I had an idea in my head: a voronoi grid modified to have rounded cells that change in size. I made an attempt here for single cells changing size. The next step was to merge cells together, as I had done on this project. I decided that the way to demo this would be to simulate some kind of belief/cultural systems that spread over time across a map. I tried this here.

It didn't go well.
What happened? I think the problem was that I had three unknown elements in this project:
- Simulation with the simplest rendering code I could get away with. Figure out what simulation rules are interesting and cool.
- Rendering isolines on a triangle mesh.
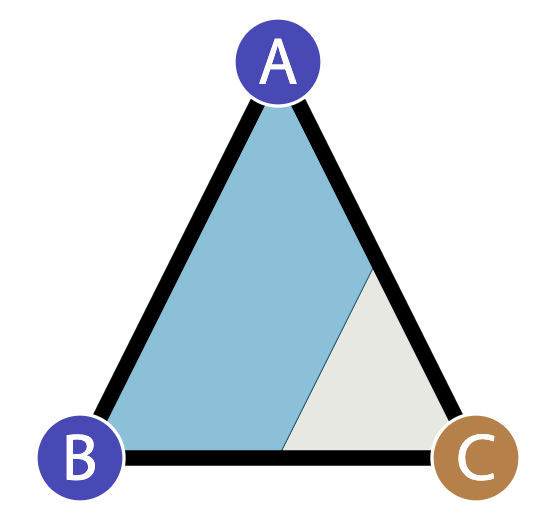
- Rendering curved isolines on a triangle mesh, using Bezier curves.
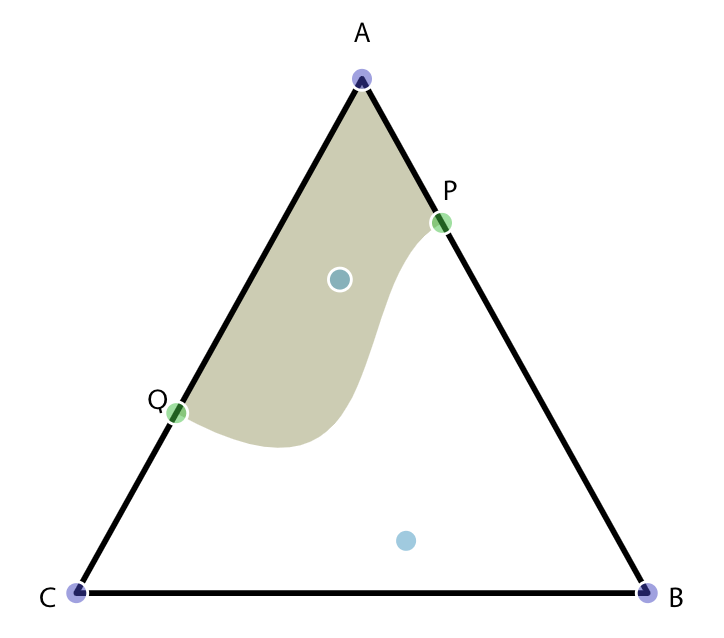
In trying to figure out all three at once, I didn't do a good job on them. I should have instead focused on one at a time. I ended up succeeding with #2 when I learned about and implemented the Meandering Triangles algorithm, and also built a little interactive visualization that helped me understand how the algorithm works. I failed with #1, having tried several algorithms but not finding one that I liked. I realized towards the end of the week that #1 was a red herring; I didn't need a simulation at all, as I really just wanted curved regions. I also failed at #3, having tried some experiments but never finding what I wanted, and also rejecting Chaikin Curves for reasons I can't remember. Since I really wanted the curved variable sized regions, I should have spent more time on #3 and less on #1. I ran out of time on this project so I'll leave #1 and #3 for another day.
You can see the animation I ended up with.
What do I mean “I ran out of time”? That's the next blog post!
Labels: triangles
Thanks Monstrim!
Post a Comment